NGUYÊN HÀM
1) Khái niệm.
Định nghĩa. Cho hàm số 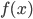 xác định trên K (K là đoạn, khoảng, nửa khoảng). Hàm số
xác định trên K (K là đoạn, khoảng, nửa khoảng). Hàm số 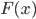 được gọi là nguyên hàm của hàm số
được gọi là nguyên hàm của hàm số 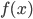 trên K, nếu
trên K, nếu 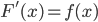 , với mọi
, với mọi 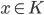 .
.
Định lý. Giả sử 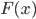 là một nguyên hàm của hàm số
là một nguyên hàm của hàm số 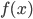 trên khoảng K. Khi đó
trên khoảng K. Khi đó
- Với mỗi hằng số C, hàm số
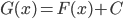 cũng là một nguyên hàm của
cũng là một nguyên hàm của 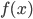 .
. - Ngược lại, nếu G(x) là một nguyên hàm của
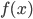 thì tồn tại hằng số C sao cho G(x) = F(x) + C.
thì tồn tại hằng số C sao cho G(x) = F(x) + C. - Họ tất cả các nguyên hàm của
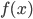 là
là 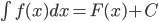 , trong đó
, trong đó 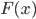 là một nguyên hàm của
là một nguyên hàm của 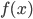 , C là hằng số bất kỳ.
, C là hằng số bất kỳ.
Nguyên hàm của một số hàm số thường gặp
| Nguyên hàm các hàm số sơ cấp thường gặp | Nguyên hàm của hàm số hợp 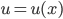 |
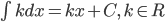 |
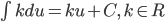 |
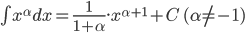 |
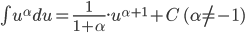 |
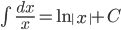 ( (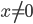 ) ) |
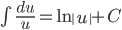 ( (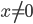 ) ) |
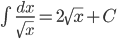 |
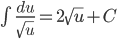 |
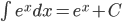 |
|
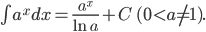 |
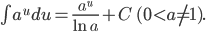 |
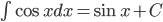 |
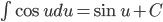 |
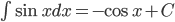 |
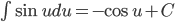 |
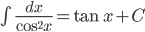 ; ; 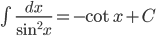 . . |
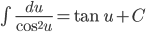 ; ; 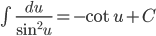 |
| Ngoài ra còn một số công thức thường gặp là.
|
|
Một số tính chất cơ bản của nguyên hàm
Định lý. Nếu 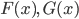 tương ứng là một nguyên hàm của
tương ứng là một nguyên hàm của 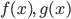 thì:
thì:
1. 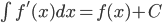
2. 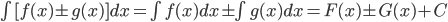 ;
;
3. 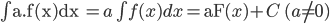 .
.
2) Một số phương pháp tìm nguyên hàm
1. Phương pháp đổi biến số
Cơ sở của phương pháp đổi biến số là định lý sau: Cho hàm số 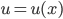 có đạo hàm liên tục trên K và hàm số
có đạo hàm liên tục trên K và hàm số 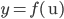 liên tục sao cho
liên tục sao cho 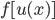 xác định trên K. Khi đó nếu F là một nguyên hàm của f, tức là
xác định trên K. Khi đó nếu F là một nguyên hàm của f, tức là 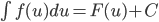 thì
thì 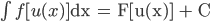 .
.
2. Phương pháp nguyên hàm từng phần
Một số dạng thường gặp:
Dạng 1. 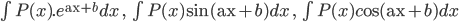
Cách giải: Đặt 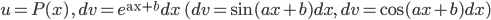
Dạng 2. 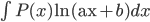
Cách giải: Đặt 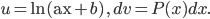
TÍCH PHÂN
1) Định nghĩa.
Cho hàm 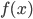 liên tục trên khoảng K và a, b là hai số bất kỳ thuộc K. Nếu
liên tục trên khoảng K và a, b là hai số bất kỳ thuộc K. Nếu 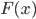 là một nguyên hàm của
là một nguyên hàm của 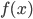 thì hiệu số
thì hiệu số 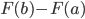 được gọi là tích phân của
được gọi là tích phân của 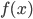 từ a đến b và ký hiệu là
từ a đến b và ký hiệu là 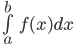 . Trong trường hợp
. Trong trường hợp 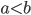 thì
thì 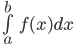 là tích phân của f trên
là tích phân của f trên 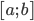 .
.
2) Tính chất của tích phân
Cho các hàm số 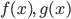 liên tục trên K và
liên tục trên K và 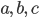 là ba số thuộc K.
là ba số thuộc K.
1.
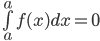
2.
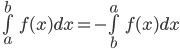
3.
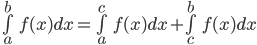
4.
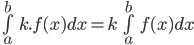
5.
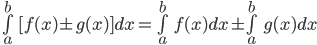
3) Một số phương pháp tính tích phân
1. Phương pháp đổi biến số: Công thức đổi biến số 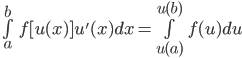 . Trong đó
. Trong đó 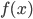 là hàm số liên tục và
là hàm số liên tục và 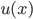 có đạo hàm liên tục trên khoảng J sao cho hàm hợp
có đạo hàm liên tục trên khoảng J sao cho hàm hợp 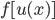 xác định trên J;
xác định trên J; 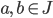 .
.
Phương pháp đổi biến số thường áp dụng theo hai cách
Cách 1. Đặt ẩn phụ 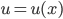 (
( 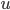 là một hàm của x)
là một hàm của x)
Cách 2. Đặt ẩn phụ
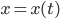
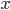 là một hàm số của t).
là một hàm số của t).
2. Phương pháp tích phân từng phần.
Định lý. Nếu 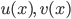 là hai hàm số có đạo hàm liên tục trên khoảng K và
là hai hàm số có đạo hàm liên tục trên khoảng K và 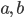 là hai số thuộc K thì
là hai số thuộc K thì 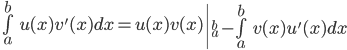
Ứng dụng của tích phân
1) Tính diện tích hình phẳng
- Nếu hàm số
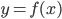 liên tục trên
liên tục trên 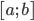 thì diện tích S của hình phẳng giới hạn bởi đồ thị hàm số
thì diện tích S của hình phẳng giới hạn bởi đồ thị hàm số 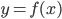 , trục hoành và hai đường thẳng
, trục hoành và hai đường thẳng 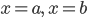 là
là 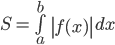 .
. - Diện tích hình phẳng giới hạn bởi các đồ thị hàm số
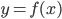 ,
, 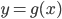 và hai đường thẳng
và hai đường thẳng 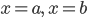 là
là 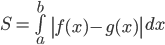
2) Tính thể tích vật thể.
- Thể tích vật thể B giới hạn bởi hai mặt phẳng vuông góc với trục Ox tại các điểm
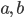 là
là 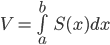 . Trong đó S(x) là diện tích thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ là
. Trong đó S(x) là diện tích thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ là 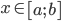 và S(x) là một hàm liên tục.
và S(x) là một hàm liên tục.
3) Tính thể tích khối tròn xoay.
- Hàm số
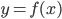 liên tục và không âm trên
liên tục và không âm trên 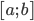 . Hình phẳng giới hạn bởi đồ thị hàm số
. Hình phẳng giới hạn bởi đồ thị hàm số 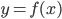 , trục hoành và hai đường thẳng
, trục hoành và hai đường thẳng 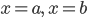 quay quanh trục hoành tạo nên một khối tròn xoay. Thể tích V được tính bởi công thức
quay quanh trục hoành tạo nên một khối tròn xoay. Thể tích V được tính bởi công thức 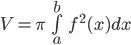 .
.
Hình phẳng giới hạn bởi đồ thị hàm số 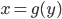 , trục tung và hai đường thẳng
, trục tung và hai đường thẳng 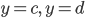 quay quanh trục tung tạo nên một khối tròn xoay. Thể tích V được tính bởi công thức
quay quanh trục tung tạo nên một khối tròn xoay. Thể tích V được tính bởi công thức 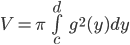 .
.
Nguyễn Thành Đô
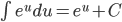

bài viết chua co vi du minh hoa