PHẦN I : Lý thuyết cơ bản :
1) Định nghĩa :
Cho hàm số f(x) xác định trên khoảng (a;b).
* Hàm số f(x) liên tục tại x0 thuộc (a;b) nếu ![]() .
.
* Hàm số f(x) liên tục trên khoảng (a;b) nếu f(x) liên tục tại mọi điểm thuộc (a;b).
* Hàm số f(x) liên tục trên đoạn [a;b] nếu f(x) liên tục trên khoảng (a;b); và ![]() ,
, ![]()
2) Các phép toán :
* Nếu f và g là 2 hàm số liên tục tại x thì các hàm số f+g, f-g, f.g cũng liên tục tại x, và nếu g(x)≠0 thì f/g liên tục tại x.
* Nếu hàm số f liên tục tại x và hàm g liên tục tại y=f(x) thì hàm hợp g.f liên tục tại x.
3) Tính chất :
Định lý 1: Nếu hàm f liên tục tại a và f(a)≠0 thì có một lân cận U(a) của a sao cho mỗi x thuộc về lân cận đó thì f(x) cùng dấu với f(a).
Định lý 2 : Nếu hàm số f liên tục trên [a;b] thì f bị chặn trên đoạn [a;b]
Định lý 3 : Nếu hàm số f liên tục trên [a;b] thì f đạt được giá trị lớn nhất nhỏ nhất trên đoạn đó.
Định lý 4 : Nếu hàm số f liên tục trên [a;b] và f (a).f(b)<0 thì có ít nhất một giá trị c thuộc khoảng (a;b) sao cho f(c)=0
Định lý 5 : Nếu hàm số f liên tục trên [a;b] và f (a)=A, f(b)=B. Lúc đó nếu C là số nằm giữa A và B thì có ít nhất một giá trị c thuộc khoảng (a;b) sao cho f(c)=C.
Định lý 6 : Nếu hàm số f liên tục trên [a;b] thì f nhận mọi giá trị trung gian giữa giá trị nhỏ nhất m và gía trị lớn nhất M của nó trên đoạn đó.
PHẦN II : Các vấn đề giải toán :
Định hướng 1 : Bài toán chứng minh phương trình f(x)=0 có nghiệm
Ta xét hàm số f(x), kiểm tra tính chất liên tục. Trên miền liên tục đó, tìm chọn 2 giá trị a,b phân biệt mà f(a)f(b)≤0, từ đó lý luận đến điều phải chứng minh.
Lưu ý :
- Nếu có
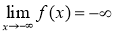 thì tồn tại
thì tồn tại 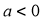 , sao cho
, sao cho 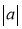 đủ lớn và
đủ lớn và 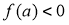
- Nếu có
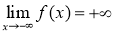 thì tồn tại
thì tồn tại 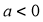 , sao cho
, sao cho 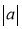 đủ lớn và
đủ lớn và 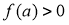
- Nếu có
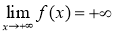 thì tồn tại
thì tồn tại 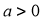 đủ lớn sao cho
đủ lớn sao cho 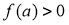
- Nếu có
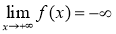 thì tồn tại
thì tồn tại 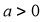 đủ lớn sao cho
đủ lớn sao cho 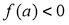
Định hướng 2 : Bài toán chứng minh phương trình f(x)=g(x) có nghiệm
Cách 1 : Xét hàm số h(x)=f(x)-g(x) như định hướng 1
Cách 2 : Nếu phương trình dạng A(x)/B(x) =C(x) , ta biến đổi về dạng
A(x)/B(x) - C(x) =0 hoặc A(x) - B(x)C(x) =0 với điều kiện B(x)≠0. Đôi khi ta còn biến đổi tương đương theo nhiều cách khác, chẳng hạn nâng lũy thừa, lấy căn thức của 2 vế phương trình...( chú ý điều kiện xác định và điều kiện có nghiệm)
Định hướng 3 : Bài toán chứng minh tồn tại số c thỏa mãn một đẳng thức
Ta có thể thay thế c bởi biến x và đưa đẳng thức về dạng phương trình có ẩn số x. Bài toán trở về bài toán theo định hướng 1 hoặc 2.
Bài tập :
Bài 1 : Chứng minh phương trình m(x-3)(x-5)+x2 -15=0 luôn có nghiệm với mọi m.
Hướng dẫn :
Xét hàm số ![]() , khi đó hàm số
, khi đó hàm số ![]() xác định và liên tục trên R. Mặt khác
xác định và liên tục trên R. Mặt khác ![]() nên tồn tại
nên tồn tại ![]() sao cho
sao cho ![]() , hay phương trình luôn có nghiệm khi m thay đổi.
, hay phương trình luôn có nghiệm khi m thay đổi.
Bài 2 : Chứng minh phương trình ab(x-a)(x-b)+bc(x-b)(x-c)+ca(x-c)(x-a)=0 luôn có nghiệm với mọi a,b,c.
Hướng dẫn :
Đặt ![]() , ta có
, ta có ![]() xác định và liên tục trên R, và :
xác định và liên tục trên R, và : ![]()
![]()
![]()
Suy ra ![]()
- Nếu
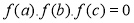 , thì một trong ba giá trị a,b,c là nghiệm của phương trình
, thì một trong ba giá trị a,b,c là nghiệm của phương trình 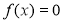 .
. - Nếu
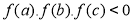 thì tồn tại
thì tồn tại 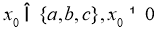 và
và 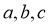 khác 0 sao cho
khác 0 sao cho 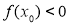 , mà
, mà 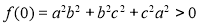 nên
nên 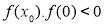 do đó phương trình
do đó phương trình 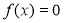 có nghiệm
có nghiệm
Bài 3 : Chứng minh các phương trình sau có nghiệm :
a) 3x+4x=8x b) sinx +1 = x
Hướng dẫn :
a) Xét hàm số ![]() , khi đó hàm số
, khi đó hàm số ![]() xác định và liên tục trên R. Mặt khác
xác định và liên tục trên R. Mặt khác ![]() nên tồn tại
nên tồn tại ![]() sao cho
sao cho ![]() , hay phương trình luôn có nghiệm.
, hay phương trình luôn có nghiệm.
b) Xét hàm số ![]() , khi đó hàm số
, khi đó hàm số ![]() xác định và liên tục trên R. Mặt khác
xác định và liên tục trên R. Mặt khác ![]() nên tồn tại
nên tồn tại ![]() sao cho
sao cho ![]() , hay phương trình luôn có nghiệm.
, hay phương trình luôn có nghiệm.
Bài 4 : Chứng minh các phương trình sau luôn có nghiệm với mọi tham số
1) 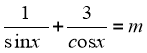 , m là tham số .
, m là tham số .
2) ![]() với a,b,c là tham số
với a,b,c là tham số
Hướng dẫn :
1) Xét hàm số ![]() , khi đó hàm số
, khi đó hàm số ![]() xác định và liên tục trên
xác định và liên tục trên 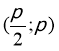 .
.
Ta có 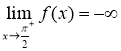 nên tồn tại
nên tồn tại ![]() sao cho
sao cho ![]()
và ![]() nên tồn tại
nên tồn tại ![]() sao cho
sao cho ![]()
với ![]() đủ bé sao cho
đủ bé sao cho ![]() .
.
Do đó ![]() nên tồn tại
nên tồn tại ![]() sao cho
sao cho ![]() , hay phương trình luôn có nghiệm.
, hay phương trình luôn có nghiệm.
2) Xét hàm số ![]() , khi đó hàm số
, khi đó hàm số ![]() xác định và liên tục trên R.
xác định và liên tục trên R.
Ta có : ![]()
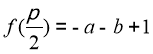
![]()
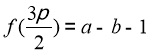
Nên 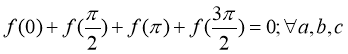 do đó tồn tại hai giá trị
do đó tồn tại hai giá trị ![]() thuộc
thuộc 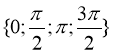 sao cho
sao cho ![]() hay phương trình luôn có nghiệm.
hay phương trình luôn có nghiệm.
Bài 5 : Cho 3 số a,b,c thoả 12a+15b+20c =0 . Chứng minh phương trình ![]() luôn có nghịêm thụôc đọan
luôn có nghịêm thụôc đọan ![]()
Hướng dẫn :
Xét hàm số ![]() , khi đó hàm số
, khi đó hàm số ![]() xác định và liên tục trên R.
xác định và liên tục trên R.
Ta có : 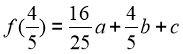 nên
nên 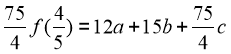
![]() nên
nên 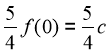
do đó 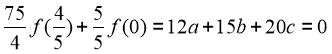 suy ra một trong hai giá trị
suy ra một trong hai giá trị 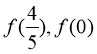 có một giá trị âm và một giá trị dương, hoặc cả hai giá trị đều bằng 0.
có một giá trị âm và một giá trị dương, hoặc cả hai giá trị đều bằng 0.
Từ kết quả trên ta có phương trình ![]() luôn có nghiệm
luôn có nghiệm
Bài 6 : Cho 3 số a,b,c thoả 5a+4b+6c =0 . Chứng minh phương trình ![]() luôn có nghịêm.
luôn có nghịêm.
Hướng dẫn :
Xét hàm số ![]() , khi đó hàm số
, khi đó hàm số ![]() xác định và liên tục trên R.
xác định và liên tục trên R.
Ta có : ![]() ,
, ![]() ,
, 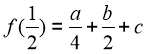
do đó 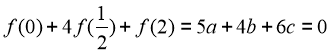
suy ra tồn tại hai giá trị ![]() thuộc
thuộc 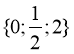 sao cho
sao cho ![]()
hay phương trình luôn có nghiệm.
Bài 7 : Cho f là hàm số xác định và liên tục trên R . CMR nêú f (0)=f(1) và vơí m nguyên dương bất kỳ thì phương trình ![]() có nghịêm.
có nghịêm.
Hướng dẫn :
Đặt ![]() khi đó hàm số
khi đó hàm số ![]() xác định và liên tục trên R.
xác định và liên tục trên R.
Ta có :
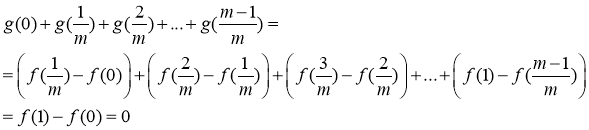
- Nếu
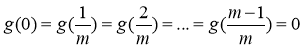 thì phương trình
thì phương trình 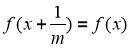 có nghịêm.
có nghịêm. - Nếu các giá trị
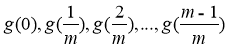 không đồng thời bằng 0 thì tồn tại hai số
không đồng thời bằng 0 thì tồn tại hai số 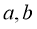 thuộc
thuộc 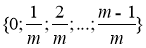 thỏa
thỏa 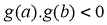 hay phương trình
hay phương trình 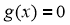 có nghiệm, suy ra phương trình
có nghiệm, suy ra phương trình 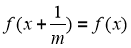 có nghịêm.
có nghịêm.
![]()
TỔ TOÁN
Gửi bình luận