CÁC DẠNG TOÁN THƯỜNG GẶP
Phần 1. Tìm nguyên hàm
Dạng 1: Tìm nguyên hàm dựa vào bảng nguyên hàm .
Bài 1. Tìm nguyên hàm của các hàm số
a. ![]() b.
b. ![]() c.
c. ![]()
d. ![]() e.
e. ![]() f.
f. ![]()
g. ![]() h.
h. ![]() i.
i. 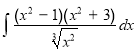
k. 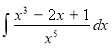 l.
l. ![]() m.
m. ![]()
n. ![]() o.
o. ![]() p.
p. ![]()
Dạng 2. Tìm nguyên hàm bằng phương pháp đổi biến.
Tính tích phân ![]()
Phương pháp 1. Đổi biến ![]() , rút x theo t.
, rút x theo t.
+) Xác định vi phân: ![]()
+) Biểu thị f(x)dx theo t và dt. Giả sử ![]() . Khi đó
. Khi đó ![]()
Lưu ý: Một số dấu hiệu dẫn tới việc lựa chọn ẩn phụ:
|
Dấu hiệu |
Có thể chọn |
|
Hàm số có mẫu |
Đặt t là mẫu |
|
Hàm |
Đặt |
|
Hàm |
Đặt |
|
Hàm |
Đặt |
|
Hàm lẻ với sinx |
Đặt |
|
Hàm lẻ với cosx |
Đặt |
|
Hàm chẵn với sinx và cosx |
t =tanx |
Phương pháp 2. Đổi biến ![]()
+) Lấy vi phân ![]()
+) Biểu thị f(x) theo t và dt, Giả sử: f(x)dx= g(t)dt. Khi đó ![]()
Lưu ý: Một số dấu hiệu dẫn tới việc chọn ẩn phụ:
|
Dấu hiệu |
Có thể chọn |
|
|
|
|
|
|
|
|
|
|
|
Đặt |
|
|
Đặt |
Bài 2. Tìm nguyên hàm của các hàm số
a. ![]() b.
b. ![]() c.
c. ![]()
d. ![]() e.
e. ![]() f.
f. ![]()
g. ![]() h.
h. ![]() k.
k. ![]()
l. ![]() m.
m. ![]() n.
n. ![]()
o. ![]() p.
p. ![]() q.
q. ![]()
r. ![]() s.
s. ![]() t.
t. ![]()
u. ![]() v.
v. ![]()
Dạng 3. Tìm nguyên hàm bằng phương pháp từng phần.
Bài 3. Tìm nguyên hàm của các hàm số.
a. ![]() b.
b. ![]() c.
c. ![]()
d. ![]() e.
e. 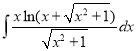 f.
f. ![]()
g. ![]() h.
h. ![]()
Dạng 4. Nguyên hàm của một số hàm phân thức hữu tỷ.
Bài 4. Tìm nguyên hàm
a. ![]() b.
b. ![]() c.
c. ![]()
d. ![]() e.
e. ![]() f.
f. ![]()
g. ![]() h.
h. ![]() h.
h. ![]()
i. ![]() k.
k. ![]() l.
l. ![]()
Dạng 5. Nguyên hàm của một số hàm số lượng giác.
Các bài toán cơ bản:
a) Nguyên hàm của các hàm số có dạng:
![]()
Phương pháp chung: Dùng các công thức biến đổi, công thức hạ bậc để đưa về tổng các nguyên hàm cơ bản.
Bài 5. Tìm các nguyên hàm:
a.![]() b.
b. ![]() c.
c. ![]()
b) Nguyên hàm của các hàm số có dạng: ![]()
Phương pháp chung: Dựa vào tính chẵn lẻ của m, n để biến đổi hoặc đặt ẩn phụ cho phù hợp.
Bài 6. Tìm nguyên hàm
a. ![]() b.
b. ![]() c.
c. ![]()
d. ![]() e.
e. ![]() f.
f. ![]()
g. ![]() h.
h. ![]()
Dạng 6. Tìm nguyên hàm bằng phương pháp đổi biến lượng giác.
Bài 7. Tìm nguyên hàm
a. ![]() b.
b. ![]() c.
c. ![]()
d. ![]() e.
e. ![]() f.
f. ![]()
g. ![]() h.
h. 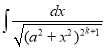 k.
k. ![]()
l. ![]() với (
với (![]() ) m.
) m. ![]() n.
n.![]()
Bài 8. Tìm nguyên hàm
a. 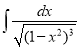 b.
b. ![]() c.
c. 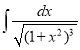
d. ![]() e.
e. ![]() f.
f. ![]()
g. 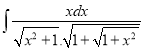 h.
h. ![]()
Dạng 7. Nguyên hàm của một số hàm số mũ và lôgarit
Bài 9. Tìm nguyên hàm
a. ![]() b.
b. ![]() c.
c. ![]()
d. ![]() e.
e. ![]() f.
f. ![]()
Phần 2. Tính tích phân
- Dạng 1. Dùng định nghĩa và các tính chất của tích phân.
Bài 10. Tính các tích phân
a. ![]() b.
b. ![]() c.
c. 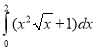
d. ![]() e.
e. 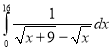 f.
f. 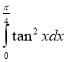
g. 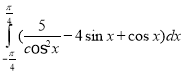 h.
h. 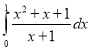 i.
i. 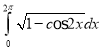
k. 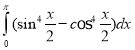 l.
l. 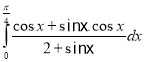 m.
m. 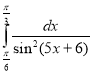
n. 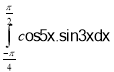 o.
o. 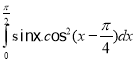 p.
p. ![]()
- Dạng 2. Tính tích phân bằng phương pháp phân tích
Bài 11. Tính tích phân
a. 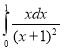 b.
b. 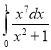 c.
c. 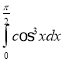
d. 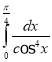 e.
e. 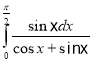 f.
f. 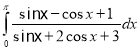
g. 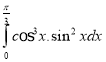 h.
h. ![]()
- Dạng 3. Tính tích phân bằng phương pháp đổi biến.
Bài 12. Tính các tích phân sau
a. ![]() b.
b. 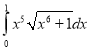 c.
c. 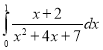
d. 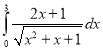 e.
e. 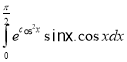 f.
f. 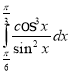
g. 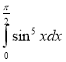 h.
h. 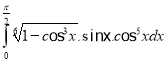 i.
i. ![]()
k. 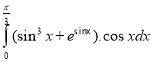 l.
l. 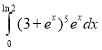 m.
m. 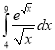
Bài 13. Tính các tích phân
a. 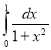 b.
b. 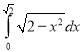 c.
c. 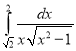
d. 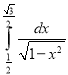 e.
e. 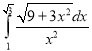 f.
f. 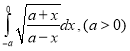
g. 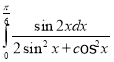 h.
h. 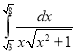
Bài 14. Tính các tích phân
a. ![]() b.
b. 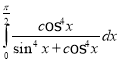 c.
c. ![]()
d. 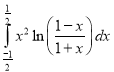 e.
e. 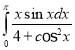 f.
f. ![]()
g. 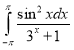 h.
h. 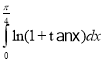 i.
i. 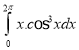
k. 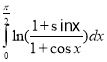 l.
l. 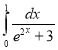 m.
m. 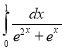 .
.
- Dạng 4. Tính tích phân bằng phương pháp tích phân từng phần.
Bài 15. Tính các tích phân
a. 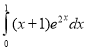 b.
b. ![]() c.
c. 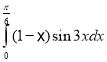
d. 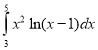 e.
e. 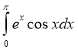 f.
f. 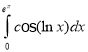
g. ![]() h.
h. 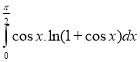
- Dạng 5. Liên kết phương pháp đổi biến số và tích phân từng phần
Bài 16. Tính tích phân
a.  b.
b. 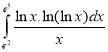 c.
c. 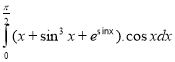
- Dạng 6. Lập công thức tích phân truy hồi
Bài 17. Lập công thức tích phân truy hồi cho các tích phân sau.
a. 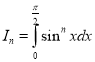 b.
b. 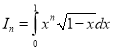 với n là số nguyên dương.
với n là số nguyên dương.
• Dạng 7. Ứng dụng của tích phân
Bài 18. Tính diện tích hình phẳng được giới hạn bởi đồ thị của các hàm số sau.
a. ![]() và trục hoànhb.
và trục hoànhb. ![]() và đường thẳng
và đường thẳng ![]()
c. ![]() ;
; ![]() và
và ![]() d.
d. ![]()
e. ![]() f.
f. ![]()
Bài 19. Tính thể tích khối tròn xoay khi quay quanh trục mỗi hình phẳng giới hạn bởi.
a. ![]() ; trục hoành và hai đường thẳng
; trục hoành và hai đường thẳng ![]() .
.
b. ![]() , trục hoành và đường thẳng
, trục hoành và đường thẳng ![]()
c. ![]()
d. ![]() .
.
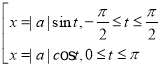
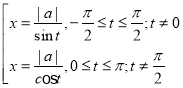
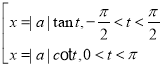
hiểu
hay
K có lời giải ạ
đáp án đâu ạ